A section of a
fiber bundle gives an element of the fiber over every point in
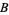
. Usually it is
described as a map
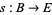
such that
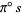
is the
identity on
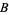
. A real-valued function on a manifold
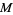
is a section of the trivial
line
bundle 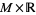
. Another common example is a
vector field, which is a section of the
tangent
bundle.
The rank of a
vector bundle is the
dimension of its
fiber. Equivalently, it is the maximum number of
linearly independent
local bundle
sections in a
trivialization. Naturally, the
dimension here is measured in the appropriate
category.
For instance, a real line bundle has fibers isomorphic with
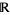
, and a complex
line bundle has fibers isomorphic to
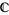
, but in both cases
their rank is 1.
The rank of the
tangent bundle of a real
manifold 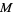
is equal to the dimension of
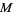
. The rank of a
trivial bundle
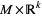
is equal to
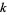
. There is no upper
bound to the rank of a vector bundle over a fixed manifold
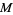
.
Source :
WMW